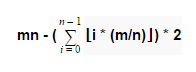SLOG #11

    During the last week of class, we were presented with a difficult mathematical problem "diagonals". I attempted to solve this problem with a friend, whose solution is posted at http://dingtaoliu.blogspot.ca/2014/12/during-last-csc165-class-i-worked-on.html. He gave me critical insights in approaching the problem by suggesting the connection between this problem and the concept of integrals. I applaud the extraordinary perspective he chooses to tackle this problem.

1. Understand the problem.

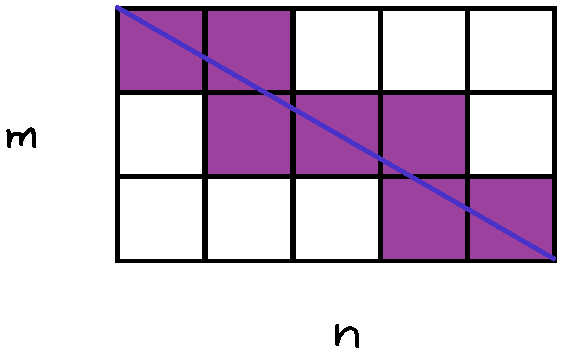
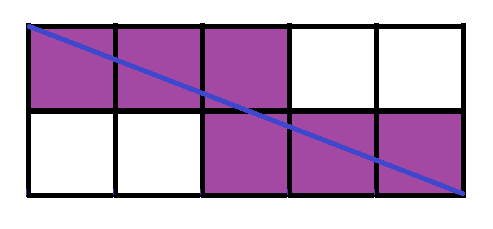
Problem: A rectangular grid made up of m rows and n columns (m and n are both positive integers) has a line drawn from its top left corner to its bottom right corner (the diagonal). Given m and n, derive a formula that calculates how many squares the line passes through. Below is an illustration of the problem when m = 3 and n = 5.

The purple squares indicate those that the line passed through. In this case, the line passes through 7 squares.

So, in essence, we are given two variables, m and n, and we are asked to produce one output, the number of squares passed through by the line.

2. Devising a plan.

I have not seen, or perhaps I have, and I just forgot, a problem similar to this, but one approach to solve it immediately comes to mind.

Plan A:

    Start with small examples. Hold one variable constant and keep changing the other variable by 1, maybe a clear pattern will surface.

Professor Heap mentioned that it actually doesn't matter if the line is drawn from top left to bottom right, or from top right to bottom left, because the number of sliced squares will be the same. This prompts the approach to view the rectangular grid as two identical triangles. If we figure out the number of sliced squares inside one triangle, then we would know the number of sliced squares inside the rectangular grid.

Plan B:

    View the rectangular grid as two identical triangles. It can be difficult to account for exactly how many whole squares are sliced, that is, how many whole squares can the sliced parts along the hypotenuse of the triangle make up. Moreover, there is also the possibility of an extra part dangling on its own because its counterpart is in the other triangle. Therefore, we decided that we should try to calculate the number of  whole squares inside a triangle, that is, the number of squares that do not touch the diagonal line. Then, a simple subtraction, total number of squares - (number of untouched squares in a triangle)*2, can get us the answer we are looking for.

3. Carrying out the plan.

Plan A:

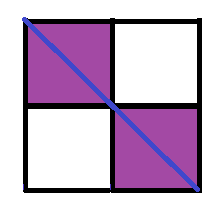
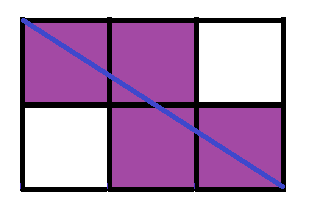
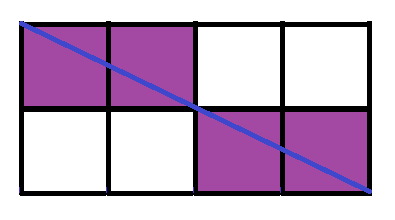
    Plan A was fairly easy to begin. I started out by drawing 2 by 2 rectangle grids, then increased the length by 1 for a few times, as illustrated below.

First:

2 sliced squares

Second:

4 sliced squares

Third:

4 sliced squares

Fourth:

6 sliced squares

So, the pattern seems to be that starting from 2, for every increase of 2 on the length, the number of sliced squares increases by 2. Now try with various widths.

First:

6 sliced squares

Second:

7 sliced squares

Third:

8 sliced squares

Okay, so the number of sliced squares seems to be increasing by 1 for every increase in width. At this point, intuition tells that it can be very difficult to come up with a pattern that encompass two variables by drawing pictures with, in reality, only one variable. Any apparent consequent pattern about the change in either length, or width(only one at a time) is inconclusive, especially with the fact that the illustrations can be rotated ninety degrees, and then the pattern for previous length does not apply for the "new" length. 

Plan B:

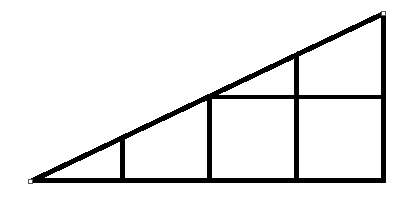
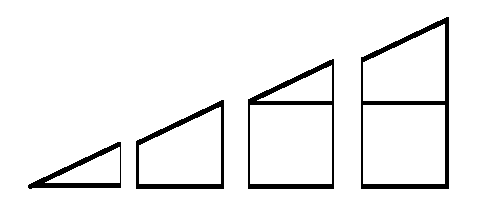
    Perhaps the most difficult part of this plan was finding a way to distinguish the whole squares from the incomplete squares. My friend's observation of the problem's resemblance to integration has significantly advanced our progress. The connection is shown below.

This:

Becomes:

    Then, it is clear to see how to calculate the number of complete squares inside the triangle; all we need to do is look at the shorter side of each shape, and the floor of that length will produce the number of complete squares inside that shape. The length of each side of the shape can be written as a function to its place (starting from 0) in the triangle as f(x) = mx, where m is the slope of the hypotenuse of the triangle. So for the example above, the slope can be calculated by rise over run: 2 / 4 = (1/2). Then, the shortest side for the first shape is at position 0, thus its height is f(0) = (1/2)(0)=0. Then we know there is no complete square in the first shape. For the second shape, f(1) = 1/2, and the floor of 1/2 is 0, so there is still no square. For the third one, f(2) = 1, and floor(1) = 1, so there is one square present. Lastly, for the fourth one, f(3) = 3/2, and floor(3/2) = 1, so there is one square. In total, we have seen 2 complete squares. Since the total number of squares in a 4 by 2 rectangular grid is 4*2 = 8, then the number of sliced squares, (the formula was mentioned in Devising a plan: Plan B) 8 - 2(2) = 4.

We used summation to devise a formula that represents this method:

Where m is the width of the rectangular grid, and n is the length of the rectangular grid. Note that this formula only works if the diagonal line is drawn from the bottom left corner to the top right corner, so the shorter length of each shape inside the triangle is calculated.

4. Looking back

    We can check the result by plugging in m and n for a few examples shown in Carrying out the plan: Plan A.

    For a 2 by 2 rectangle, the formula gives us 2 * 2 - (⌊0 * (2/2)⌋ + ⌊1 * (2/2)⌋) * 2 = 2, which matches the illustration.

For a 3 by 2 rectangle, the formula gives us 3 * 2 - (⌊0 * (2/3)⌋ + ⌊1 * (2/3)⌋ + ⌊2 * (2/3)⌋) * 2 = 4, which matches the illustration.

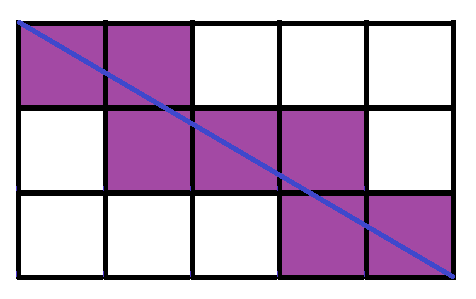
For a 5 by 3 rectangle, the formula gives us 5 * 3 - (⌊0 * (3/5)⌋ + ⌊1 * (3/5)⌋ + ⌊2 * (3/5)⌋ + ⌊3 * (3/5)⌋ + ⌊4 * (3/5)⌋) * 2 = 7, which matches the illustration.

    We tunneled through to this solution once we figured out how to calculate the number of complete squares inside a triangle, so we probably would not have reached the same solution easily with another approach.

    Similar methods can be used to solve this type of problem encountered in computer graphics or video game design that involve the particular concept of this problem.

SLOG #10

    This week the professor talked about the idea that not all problems of mathematical nature can be solved using computers programs that humans can write. We were given an example that involved predicting if a program will terminate, whether reaching the end of its algorithms or raising an exception during execution. The function navel_gaze was used to demonstrate that such a prediction is probably impossible. I was very confused when I read navel_gaze(navel_gaze), because I couldn't read and follow the code at all. I think the message isn't to understand exactly what's going on inside the function (know what H(f, f) will produce when f = navel_gaze()), but to make two assumptions and look at the result from those assumptions. First, assume that H(f, f) is true when f = navel_gaze(), then the program will be stuck on the while loop, therefore navel_gaze(navel_gaze) does not halt. Second, assume that H(f, f) is false when f = navel_gaze(), then the program will simply return 42. In each of the result I see a contradiction, the first assumption suggests that navel_gaze(navel_gaze) will eventually stop, but the result shows otherwise. The second assumption suggests that navel_gaze(navel_gaze) will not stop, whereas the result clearly shows an end to the program.
    The professor also talked about counting in a way that is 1 to 1 and onto, which was fairly straightforward, but things got strange when he talked about a set being countable. A method called diagonalization was used to show that the size of the set of rational numbers is the same as the size of the set of natural numbers, and that the size of the set of real numbers is bigger than the size of the set of natural numbers, but I didn't quite understand the method, and googling diagonalization made it seem more confusing. Hopefully, professor Heap will go through the proof more thoroughly in the next lecture.

SLOG #9

    This week we worked on more proofs involving big-Oh, big-Omega, and saw a glimpse of big-Theta, which probably aims to prove that a function has the same growth rate as another function, since it involves both the lower and upper bound with two different coefficients. 
    I had the most difficulty trying to understand Monday's lecture about incorporating L'Hôpital's rule into a proof. When we are asked to prove that 2^n is not in big-Oh of  n^2, it is easy to think that an exponential function with base greater than 1 probably outgrows any sort of polynomial at some point, but it's hard to intuitively view it as a limit of a ratio (2^n) / (n^2) as n approaches infinity. Using L'Hôpital's rule we were able to evaluate the limit to be positive infinity, which suggests that there is no positive real number C such that when multiplied with n^2 will produce a value that is definitely larger than 2^n on the domain of this ratio. But the result of the limit made me wonder, what if n^2 were changed to -(n^2)? Then the limit would evaluate to negative infinity. Graphically, there is no doubt that 2^n is not upper-bounded to -(n^2), since one lies above and one lies below the x-axis. So then, does the negative infinity mean we have to find some number C that is less than negative infinity (although certainly there isn't any)? What if some other limit of ratio evaluates to a negative finite number, does that mean we automatically get the disproof, given that C must be a positive real number? What if the ratio were inverted, so limit as n approaches infinity of (n^2) / (2^n)  evaluates to zero, how should we start looking for C and B?

SLOG #8

    This week we focused on calculating the upper bound of the worst case scenario for a function and of the other polynomials. The material expanded to proofs involving big-Oh of a polynomial with multiple (3) terms as the upper bound. So first we looked to simplify the original function (also a polynomial) down to one term, by raising every term contained in that function to the highest degree. We then looked to simplify the upper bound by finding new polynomials that are both smaller and contain fewer terms than the original. Eventually we were able to have the upper bound be represented by only one term, and the rest of the proof was done automatically.
    The tutorial questions from this week caused some confusion for me, because we used a formula to sum up the numbers in a sequence when counting the steps of a program, but professor Heap did not used that formula on a similar question during lecture. The example in lecture appeared as follows:
def IS(A):
    i = 1
    while i < len(A):
        t = A[i]
        j = i
        while j < 0 and A[j - 1] > t:
            A[j] = A[j - 1]
            j = j -1
        A[j] = t
        i = i + 1
    When calculating the number of times the inner loop is executed, professor Heap wrote (n - 1)(i), n being the length of the input list, and later simplified it to (n)(n). But in the tutorial, we had to find exactly how many times, for each iteration of the outer loop, the inner loop is executed. For example, the inner loop executed once when i is 1, and five times when i is 5 (that is, if i can go up to and including 5). I was quite confused by these two different methods of calculation, because I thought they served the same purpose. However, it turns out that the example in lecture was an overestimate, and the question in tutorial asks for a very precise answer. So when doing proofs of big-Oh of some program, we can quite lazily (perhaps irresponsibly?) add a few more loops to the execution of the original program as long as the result does not exceed the growth rate of the same order, for example, x^2. However, when we are asked to computer the number of steps performed by an algorithm in the worst-case, we have to make sure that the number or expression we produce actually points to the number of steps for the worst case, not some vague overestimation.

SLOG #7

    This week we covered the calculations and proofs for the upper boundary and the lower boundary of the worst case scenario for an insertion sort algorithm. Both proofs were fairly easy to follow after accepting the fact that we can find the value of a variable after it has already been introduced, and fill that value in for the assignment statement at or near the beginning of the proof. However, I imagine writing similar proofs on different algorithms to be far more difficult than just following the professor's steps, because counting the number of possible repetitions for each line can get tedious very quickly with nested while loops and boolean operators (not, and, or) inside their loop conditions.     One question I have in mind is the precision to which we calculate the boundaries. When Professor Heap did the big-Oh proof, he arrived at a step WIS(A) ≤ 1 + 5(n - 1) + 1 + (n - 1) * (3i  + 1), then he said, since n > n - 1, then it's fine to write the next line as ≤ 1 + 5n + 1 + n(3i + 1). I find this somewhat unfitting in a rigorous process such as computing the upper boundary for the steps a program takes to execute. When we arrived at the polynomial an^2 + bn + c, every term was changed to have variables raised to the highest degree, so the result was  an^2 + bn^2 + cn^2. Then, every term in that polynomial can be considered equally as important, thus when we see n - 1 as n, we may miss the actual number of steps for the worst case scenario by quite a lot. 
    For this particular example, if I wanted to expand 1 + 5(n - 1) + 1 + (n - 1) * (3i  + 1), I could write i as (n - 1), since i starts from 1 and goes up to n -1 (n being the length of the list). Then I would have
WIS(A) ≤ 2 + 5(n - 1) + (n - 1)*(3(n - 1) + 1)
WIS(A) ≤ 2 + 5n - 5 + (n - 1)*(3n -2)
WIS(A) ≤ 2 + 5n - 5 + 3n^2 -5n + 2
WIS(A) ≤ 3n^2 - 1
WIS(A) ≤ 3n^2
    So the upper boundary is actually 3n^2 instead of 11n^2, less than 30% of what was originally estimated.
    Now, as I was doing the above expansions I realized we only needed to prove an existential statement, so we need not to be so rigorous after all. Go me.
    Also I'm lost as to what the breaking point (B) of WIS(A) ≤ 3n^2 is, perhaps it's zero? In retrospect, maybe I shouldn't have expanded that polynomial.

SLOG #6

    This week we finished up the lectures on writing proofs and had a brief introduction on comparing different numbers of steps two programs take to complete a similar task. We were given the equations g(n) = n^2, f(n) = 3n^2 + 50, h(n) = 15n^2 + n, and we were told that they are all the same. That sounded quite bizarre to me because how can they be the same if the last function grew over 15 times faster than the first function. Then professor Heap's justification cleared up a lot of my confusion. He explained that since the highest degree in all of these functions are n^2, then their growth rates are relatively similar compared to something of a lower or higher degree, such as n^5.
    We ended off Friday's lecture with another problem-solving session. The problem describes a situation where a person is faced with two drawers, one being empty while the other has 64 pennies. If either one of the drawers contains an even number of pennies, then that person can take half of the pennies from that drawer and put it into the other drawer. If both drawers contain an even number of pennies, then the person can make a choice of from which drawer he should take away half the pennies and put it into the other. The question asks if  it  is possible to perform the above operations in such a way that one of the drawers ends up containing any number of pennies in range [0, 64].
    After coming up with some scenarios my intuition tells me that it is possible for the pile size in a drawer to be any number within range [0, 64], but I have no idea how to prove it. So far I have noticed that for every pile size that is equal to or smaller than 32, there is a corresponding pile size that is equal to or greater than 32, which suggests that if I could prove that pile sizes [0, 32] are feasible then pile sizes [0, 64] must also be feasible. So how can I prove pile sizes [0, 32] actually all exist? I tried to apply the concept of reducing the range again so it changes from [0, 32] -> [0, 16] -> [0, 8] -> [0, 4] -> [0, 2] -> [0, 1] so that I only have to prove pile sizes 0 and 1 exist, but I'm not very convinced that this is correct, because it's not as straight-forward as going from [0, 64] to [0, 32]; it is very clear that if one drawer has 1 penny then the other must have 63 pennies, not so clear when the range is changed around so many times. So I will have to look for another solution.

SLOG #5

    This week's material is once again focused on proofs. I found that most of the material was easy to follow and understand, though I may experience difficulties writing them out on my own. However, I still have trouble trying to figure out exactly what's going on with one of the examples in lecture.

    The problem I'm referring to is to prove that for all e in the set of positive real numbers, there is a d in the set of positive real numbers, that for all x in the set of real numbers, if |x - 3| < d, then |x^2 - 3^2| < e. I'm confused as to what the question is asking because there seems to be no relationship between e and d. How is it that the absolute value of (x - 3) is smaller than d implies the absolute value of x^2 - 3^2 is smaller than e? To understand this question better, I tried to look at it like a limit question, where I pick e first as a upper and lower bound, and then I must choose a d that is within the bounds, but not the reference point itself. This perspective helped me a little in perceiving the problem. I can sense a relationship between d and e now; I have to define a d such that for all the possible values of e, whenever |x-3| < d is true, |x^2 - 3^3| < e must be true, which means d has to be some value that depends on e in order to make the implication true. The next part that I am confused about is the content of the proof. Due to my lack of practice with absolute value inequalities, I'm not comfortable in taking numbers out of them. Specifically, I don't understand why d * |x + 3 - 3 + 3| is less than or equal to d* (|x - 3| + 6), because it looks to me that they produce the same value, so they should be equal. Also, the professor arbitrarily chose a number (1) that d is no larger than, so eventually was defined as the minimum between 1 and e/7. Does that mean I can choose any arbitrary number I like, as long as I change the denominator?

    There are still some questions left in my mind, and I will seek the answers during next week.